Back in 1996, a quantum physicist at Bell Labs in New Jersey published a new recipe for searching through a database of N entries. Computer scientists have long known that this process takes around N steps because in the worst case, the last item on the list could be the one of interest.
However,
this physicist, Lov Grover, showed how the strange rules of quantum
mechanics allowed the search to be done in a number of steps equal to
the square root of N.
That
was a big deal. Searching databases is a foundational task in computer
science, used for everything from finding telephone numbers to breaking
cryptographic codes. So any speed-up is a significant advance.
Quantum
mechanics provided an additional twist. At the time, Grover’s recipe
was only the second quantum algorithm that had been proved faster than
its classical counterpart. (The first was Peter Shor’s algorithm for
factoring numbers, which he discovered in 1994.) Grover’s work was an
important factor in preparing the way for the quantum computing
revolution that is still ongoing today.
But
despite the interest, implementing Grover’s algorithm has taken time
because of the significant technical challenges involved. The first
quantum computer capable of implementing it appeared in 1998, but the
first scalable version didn’t appear until 2017, and even then it worked
with only three qubits. So new ways to implement the algorithm are
desperately needed.
Today
Stéphane Guillet and colleagues at the University of Toulon in France
say this may be easier than anybody expected. They say they have
evidence that Grover’s search algorithm is a naturally occurring
phenomenon. “We provide the first evidence that under certain
conditions, electrons may naturally behave like a Grover search, looking
for defects in a material,” they say.
That
has obvious implications for quantum computing, but its real import may
be much more profound. For some time, theorists have debated whether
quantum search could explain one of the greatest mysteries about the
origin of life. The idea that Grover searches occur in nature could
finally solve the conundrum.
First
some background. Because it is so fundamental, Grover’s search
algorithm can be reformulated in a variety of ways. One of these is as a
quantum walk across a surface—the way a quantum particle would move
randomly from one point to another.
Clearly,
this process is a kind of search of two-dimensional space. But because a
quantum particle can explore many paths at the same time, it is much
faster than a classical search.
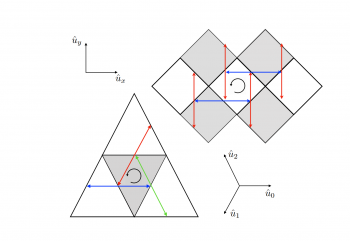
The
nature of the surface has an important influence on the search. For
example, one type of surface consists of a square grid where the quantum
particle has four possible moves at each vertex.
But
there are many other possible grids; a triangular one, for example,
where the quantum particle has three choices at each vertex. “The
triangular grid is of particular interest because of its resemblance to
several naturally occurring crystal-like materials,” say Guillet and co.
The
team focused on simulating the way a Grover search works for electrons
exploring triangular and square grids, but they also included other
physically realistic effects, such as defects in the grid in the form of
holes, and quantum properties such as interference effects.

The
results are eye-opening. The question they ask is how quickly an
electron can find the hole in a grid. And the team’s big breakthrough is
to show that these simulations reproduce the way real electrons behave
in real materials.
In
other words, this is evidence that free electrons naturally implement
the Grover search algorithm when moving across the surface of certain
crystals.
That
has immediate implications for quantum computing. “[This work] may be
the path to a serious technological leap, whereby experimentalist would
bypass the need for a full-fledged scalable and error-correcting Quantum
Computer, and take the shortcut of looking for ‘natural occurrences’ of
the Grover search instead,” say the team.
The
work also has implications for our thinking about the genetic code and
the origin of life. Every living creature on Earth uses the same code,
in which DNA stores information using four nucleotide bases. The
sequences of nucleotides encode information for constructing proteins
from an alphabet of 20 amino acids.
But why these numbers—four and 20—and not some others? Back in 2000, just a few years after Grover published his work, Apoorva Patel at the Indian Institute of Science in Bangalore showed how Grover’s algorithm could explain these numbers.
Patel’s
idea is related to the way DNA is assembled inside cells. In this
situation, the molecular machinery inside a cell must search through the
molecular soup of nucleotide bases to find the right one. If there are
four choices, a classical search takes four steps on average. So the
machinery would have to try four different bases during each assembly
step.
But
a quantum search using Grover’s algorithm is much quicker: Patel showed
that when there are four choices, a quantum search can distinguish
between four alternatives in a single step. Indeed, four is optimal
number.
This
thinking also explains why there are 20 amino acids. In DNA, each set
of three nucleotides defines a single amino acid. So the sequence of
triplets in DNA defines the sequence of amino acids in a protein.
But
during protein assembly, each amino acid must be chosen from a soup of
20 different options. Grover’s algorithm explains these numbers: a
three-step quantum search can find an object in a database containing up
to 20 kinds of entry. Again, 20 is the optimal number.
In
other words, if the search processes involved in assembling DNA and
proteins is to be as efficient as possible, the number of bases should
be four and the number of amino acids should to be 20—exactly as is
found. The only caveat is that the searches must be quantum in nature.
When
Patel published his idea, quantum physicists immediately pooh-poohed
it. At the time, they were bogged down in their own attempts to control
quantum processes, which they could do only by isolating quantum
particles in extreme environments such as at temperatures close to
absolute zero.
The
obvious problem, they said, was that living things operate in a warm,
messy environment in which quantum states would be immediately
destroyed.
Biologists were equally dismissive, saying that quantum processes couldn’t possibly be at work inside living things.
Since
then, an increasing body of evidence has emerged that quantum processes
play an important role in a number of biological mechanisms.
Photosynthesis, for example, is now thought to be an essentially quantum
process.
The
work of Guillet and co throws a new perspective on all this. It
suggests that Grover’s algorithm is not only possible in certain
materials; it seems to be a property of nature. And if that’s true, then
the objections to Patel’s ideas start to crumble.
It
may be that life is just an example of Grover’s quantum search at work,
and that this algorithm is itself a fundamental property of nature.
That’s a Big Idea if ever there was one.